La seguente definizione di statistica robusta viene dal libro di P. J. Huber, Robust Statistics.
… ogni procedura statistica dovrebbe possedere le seguenti caratteristiche desiderabili:
- Dovrebbe avere un’efficienza ragionevolmente buona (ottimale o quasi ottimale) al modello assunto.
- Dovrebbe essere robusta nel senso che piccole deviazioni dalle ipotesi del modello dovrebbero compromettere la performance solo leggermente. …
- Qualche deviazione maggiore dal modello non dovrebbe causare una catastrofe.
La statistica classica si concentra sul primo dei punti di Huber, producendo metodi che sono ottimali soggetti ad alcuni criteri. Questo post esamina gli esempi canonici usati per illustrare il secondo e il terzo punto di Huber.
Il terzo punto di Huber è tipicamente illustrato dalla media del campione (media) e dalla mediana del campione (valore medio). È possibile impostare quasi la metà dei dati di un campione su ∞ senza che la mediana del campione diventi infinita. La media del campione, d’altra parte, diventa infinita se qualsiasi valore del campione è infinito. Grandi deviazioni dal modello, cioè alcuni outlier, potrebbero causare una catastrofe per la media del campione ma non per la mediana del campione.
L’esempio canonico per discutere il secondo punto di Huber risale a John Tukey. Si inizia con il più semplice esempio da manuale di stima: dati da una distribuzione normale con media sconosciuta e varianza 1, cioè i dati sono normali(μ, 1) con μ sconosciuto. Il modo più efficiente per stimare μ è prendere la media del campione, la media dei dati.
Ma ora supponiamo che la distribuzione dei dati non sia esattamente normale(μ, 1) ma sia invece un misto di una distribuzione normale standard e una distribuzione normale con una diversa varianza. Sia δ un piccolo numero, diciamo 0,01, e supponiamo che i dati provengano da una distribuzione normale(μ, 1) con probabilità 1-δ e che i dati provengano da una distribuzione normale(μ, σ2) con probabilità δ. Questa distribuzione è chiamata “normale contaminata” e il numero δ è la quantità di contaminazione. La ragione per usare il modello normale contaminato è che si tratta di una distribuzione non normale che può sembrare normale all’occhio.
Potremmo stimare la media della popolazione μ usando la media o la mediana del campione. Se i dati fossero strettamente normali piuttosto che una miscela, la media del campione sarebbe lo stimatore più efficiente di μ. In questo caso, l’errore standard sarebbe circa il 25% più grande se usassimo la mediana del campione. Ma se i dati provengono da una miscela, la mediana campionaria può essere più efficiente, a seconda delle dimensioni di δ e σ. Ecco un grafico dell’ARE (efficienza relativa asintotica) della mediana campionaria rispetto alla media campionaria in funzione di σ quando δ = 0.01.
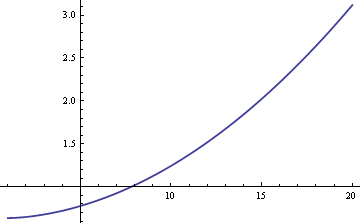
Il grafico mostra che per valori di σ maggiori di 8, la mediana del campione è più efficiente della media del campione. La superiorità relativa della mediana cresce senza limiti all’aumentare di σ.
Ecco un grafico della ARE con σ fissato a 10 e δ che varia tra 0 e 1.
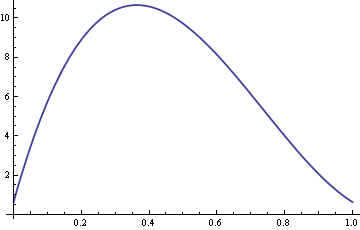
Quindi per valori di δ intorno a 0.4, la mediana campionaria è oltre dieci volte più efficiente della media campionaria.
La formula generale per l’ARE in questo esempio è 2((1 + δ(σ2 – 1)(1 – δ + δ/σ)2)/ π.
Se siete sicuri che i vostri dati sono normali senza contaminazione o con poca contaminazione, allora la media campionaria è lo stimatore più efficiente. Ma può valere la pena di rischiare di rinunciare a un po’ di efficienza in cambio di sapere che si farà meglio con un modello robusto se c’è una contaminazione significativa. C’è più potenziale di perdita usando la media del campione quando c’è una contaminazione significativa che non c’è potenziale guadagno usando la media del campione quando non c’è contaminazione.
Ecco un enigma associato all’esempio della normale contaminata. Lo stimatore più efficiente per i dati normali(μ, 1) è la media campionaria. E lo stimatore più efficiente per i dati normal(μ, σ2) è anche quello di prendere la media del campione. Allora perché non è ottimale prendere la media campionaria della miscela?
La chiave è che non sappiamo se un particolare campione proviene dalla distribuzione normale(μ, 1) o dalla distribuzione normale(μ, σ2). Se lo sapessimo, potremmo separare i campioni, fare la media separatamente, e combinare i campioni in una media aggregata: moltiplicando una media per 1-δ, moltiplicando l’altra per δ, e aggiungere. Ma poiché non sappiamo quali componenti della miscela portano a quali campioni, non possiamo pesare i campioni in modo appropriato. (Probabilmente non conosciamo nemmeno δ, ma questo è un altro discorso.)
Ci sono altre opzioni che usare la media o la mediana del campione. Per esempio, la media troncata elimina alcuni dei valori più grandi e più piccoli e fa la media di tutto il resto. (A volte gli sport funzionano in questo modo, buttando fuori i voti più alti e più bassi di un atleta dai giudici). Più dati vengono eliminati ad ogni estremità, più la media troncata si comporta come la mediana del campione. Meno dati vengono buttati via, più si comporta come la media del campione.
Post collegato: Efficienza della mediana rispetto alla media per le distribuzioni Student-t
Per consigli quotidiani sulla scienza dei dati, segui @DataSciFact su Twitter.