Gruppmultiplikation
Nu ska vi undersöka vad som händer när vi tillämpar två symmetrioperationer i följd. Som exempel kan vi betrakta molekylen \(NH_3\), som tillhör punktgruppen \(C_{3v}\). Överväg vad som händer om vi tillämpar en \(C_3\)-rotation följt av en \(\sigma_v\)-reflektion. Vi skriver denna kombinerade operation \(\sigma_v\)\(C_3\) (när de skrivs opererar symmetrioperationer på det som ligger direkt till höger om dem, precis som operatorer gör i kvantmekaniken – vi måste därför arbeta baklänges från höger till vänster från notationen för att få fram den korrekta ordningen i vilken operatörerna tillämpas). Som vi snart ska se är ordningen i vilken operationerna tillämpas viktig.
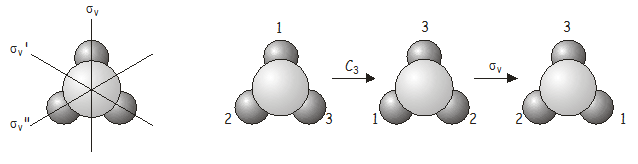
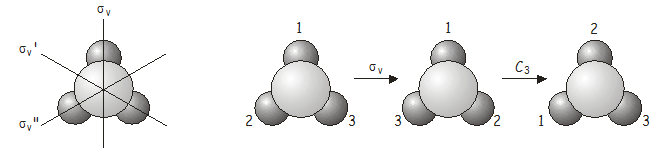
Också den kombinerade operationen \(C_3\)\(\sigma_v\) är likvärdig med en annan operation i punktgruppen, den här gången \(\sigma_v’\).
Det finns två viktiga punkter som illustreras av detta exempel:
Effekterna av att tillämpa två symmetrioperationer i följd inom en given punktgrupp sammanfattas i gruppmultiplikationstabeller. Som exempel visas nedan den fullständiga gruppmultiplikationstabellen för \(C_{3v}\) med användning av symmetrioperationer enligt definitionen i figurerna ovan. De operationer som är skrivna längs tabellens första rad utförs först, följt av de som är skrivna i den första kolumnen (observera att tabellen skulle förändras om vi valde att namnge \(\sigma_v\), \(\(\sigma_v’\) och \(\sigma_v”\) i någon annan ordning).