Följande definition av robust statistik kommer från P. J. Hubers bok Robust Statistics.
… varje statistiskt förfarande bör ha följande önskvärda egenskaper:
- Det bör ha en någorlunda god (optimal eller nästan optimal) effektivitet vid den antagna modellen.
- Det bör vara robust i den bemärkelsen att små avvikelser från modellantagandena endast bör försämra prestandan något. …
- Visst större avvikelser från modellen bör inte orsaka en katastrof.
Klassisk statistik fokuserar på den första av Hubers punkter och producerar metoder som är optimala med förbehåll för vissa kriterier. Det här inlägget tittar på de kanoniska exempel som används för att illustrera Hubers andra och tredje punkt.
Hubers tredje punkt illustreras vanligtvis av provets medelvärde (genomsnitt) och provets median (medelvärde). Man kan ställa in nästan hälften av uppgifterna i ett prov på ∞ utan att provmedianen blir oändlig. Urvalsmedelvärdet blir å andra sidan oändligt om något urvalsvärde är oändligt. Stora avvikelser från modellen, dvs. några få outliers, kan orsaka en katastrof för provets medelvärde men inte för provets median.
Det kanoniska exemplet när man diskuterar Hubers andra punkt går tillbaka till John Tukey. Börja med det enklaste läroboksexemplet på skattning: data från en normalfördelning med okänt medelvärde och varians 1, dvs. data är normal(μ, 1) med μ okänd. Det mest effektiva sättet att skatta μ är att ta stickprovets medelvärde, genomsnittet av data.
Men anta nu att datafördelningen inte är exakt normal(μ, 1) utan i stället är en blandning av en standardnormalfördelning och en normalfördelning med en annan varians. Låt δ vara ett litet tal, låt oss säga 0,01, och anta att data kommer från en normal(μ, 1)-fördelning med sannolikhet 1-δ och att data kommer från en normal(μ, σ2)-fördelning med sannolikhet δ. Denna fördelning kallas en ”kontaminerad normal” och talet δ är mängden kontaminering. Anledningen till att vi använder den kontaminerade normalmodellen är att det är en icke-normal fördelning som kan se normal ut för ögat.
Vi skulle kunna uppskatta populationens medelvärde μ med hjälp av antingen urvalets medelvärde eller urvalets median. Om uppgifterna var strikt normala snarare än en blandning skulle urvalsmedianen vara den mest effektiva skattaren av μ. I det fallet skulle standardfelet vara ungefär 25 % större om vi använde urvalsmedianen. Men om data kommer från en blandning kan urvalsmedianen vara effektivare, beroende på storleken på δ och σ. Här är en graf över ARE (asymptotisk relativ effektivitet) för urvalsmedianen jämfört med urvalsmedianen som en funktion av σ när δ = 0.01.
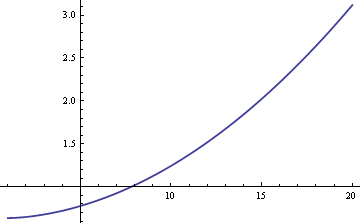
Plotten visar att för värden på σ som är större än 8 är provets median effektivare än provets medelvärde. Medianens relativa överlägsenhet växer utan gräns när σ ökar.
Här är en plott av ARE med σ fixerad till 10 och δ varierande mellan 0 och 1.
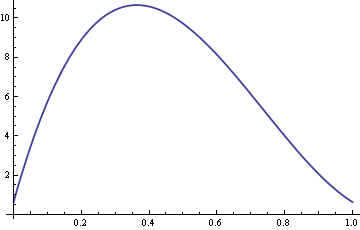
Så för värden på δ runt 0.4 är urvalsmedianen mer än tio gånger effektivare än urvalsmedelvärdet.
Den allmänna formeln för ARE i detta exempel är 2((1 + δ(σ2 – 1)(1 – δ + δ/σ)2)/ π.
Om du är säker på att dina data är normala utan kontaminering eller med mycket liten kontaminering är urvalsmedelvärdet den effektivaste skattaren. Men det kan vara värt att riskera att ge upp lite effektivitet i utbyte mot att veta att du kommer att klara dig bättre med en robust modell om det finns betydande kontaminering. Det finns en större potentiell förlust med hjälp av sampelns medelvärde när det finns en betydande kontaminering än det finns en potentiell vinst med hjälp av sampelns medelvärde när det inte finns någon kontaminering.
Här finns en gåta som är förknippad med exemplet med den kontaminerade normalvärdena. Den mest effektiva estimatorn för normal(μ, 1)-data är provmedelvärdet. Och den mest effektiva estimatorn för normal(μ, σ2)-data är också att ta stickprovsmedelvärdet. Varför är det då inte optimalt att ta stickprovsmedelvärdet av blandningen?
Nyckeln är att vi inte vet om ett visst stickprov kom från normal(μ, 1)-fördelningen eller från normal(μ, σ2)-fördelningen. Om vi visste det skulle vi kunna skilja proverna åt, göra ett genomsnitt av dem separat och kombinera proverna till ett samlat genomsnitt: multiplicera det ena genomsnittet med 1-δ, multiplicera det andra med δ och addera. Men eftersom vi inte vet vilka av blandningskomponenterna som leder till vilka prover kan vi inte väga proverna på lämpligt sätt. (Vi vet förmodligen inte heller δ, men det är en annan sak.)
Det finns andra alternativ än att använda provmedelvärde eller provmedian. Exempelvis kastar det trimmade medelvärdet ut några av de största och minsta värdena för att sedan göra ett medelvärde av allt annat. (Ibland fungerar sport på detta sätt, genom att kasta ut en idrottsutövares högsta och lägsta betyg från domarna). Ju mer data som kastas bort i varje ände, desto mer fungerar det trimmade medelvärdet som urvalsmedianen. Ju mindre data som kastas bort, desto mer fungerar det som provets medelvärde.
Relaterat inlägg: För dagliga tips om datavetenskap, följ @DataSciFact på Twitter.
>