Transportledningens ledare utgör en kondensator mellan dem. Ledarna i överföringsledningen fungerar som en parallell platta i kondensatorn och luften är precis som ett dielektriskt medium mellan dem. Kapaciteten i en ledning ger upphov till ledningsströmmen mellan ledarna. Den beror på ledarens längd.
Ledningens kapacitans är proportionell mot överföringsledningens längd. Deras effekt är försumbar på prestandan hos korta (med en längd på mindre än 80 km) och lågspänningsöverföringsledningar. När det gäller högspänningsledningar och långa ledningar anses den vara en av de viktigaste parametrarna.
Kapacitans för tvåtrådig ledning
Transmissionsledningens kapacitans bildar tillsammans med konduktanserna shuntadmittansen. Konduktansen i transmissionsledningen beror på läckaget över ledarens yta. Betrakta en ledning som består av två ledare a och b med varsin radie r. Avståndet mellan ledarna är D enligt diagrammet nedan:-
Potentialdifferensen mellan ledarna a och b är
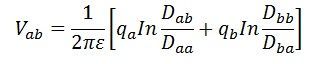Varvid qa – laddning på ledare a
qb – laddning på ledare b
Vab – potentialdifferens mellan ledare a och b
ε- absolut permittivitet
så att,
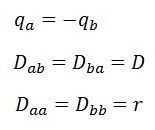Substituerar vi dessa värden i spänningsekvationen får vi,
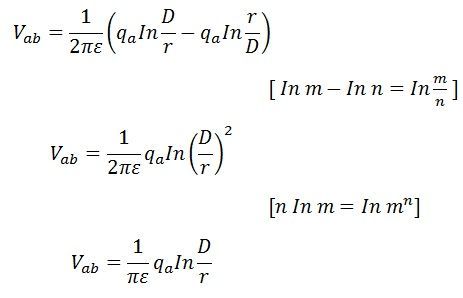Kapacitansen mellan ledarna är
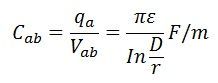Cab kallas för linje-till-linje-kapacitans.
Om de två ledarna a och b är motsatt laddade och potentialskillnaden mellan dem är noll, så ges varje ledares potential av 1/2 Vab.
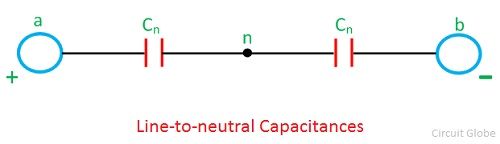Kapacitansen mellan varje ledare och nollpotentialpunkten n är
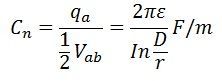Kapacitansen Cn kallas för kapacitans till neutral eller kapacitans till jord.
Kapacitansen Cab är kombinationen av två lika stora kapacitanser a och b i serie. Kapacitansen mot neutral är alltså dubbelt så stor som kapacitansen mellan ledarna, dvs,
Den absoluta permittiviteten ε ges av
där εo är det fria rummets permittivitet och εr är mediets relativa permittivitet.
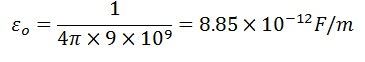För luft
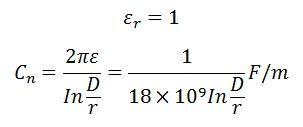Kapacitansreaktans mellan en ledare och neutral
Kapacitans för den symmetriska trefaslinjen
Låt ett balanserat spänningssystem appliceras på en symmetrisk trefaslinje som visas nedan
Fasordiagrammet för trefaslinjen med liksidigt avstånd visas nedan: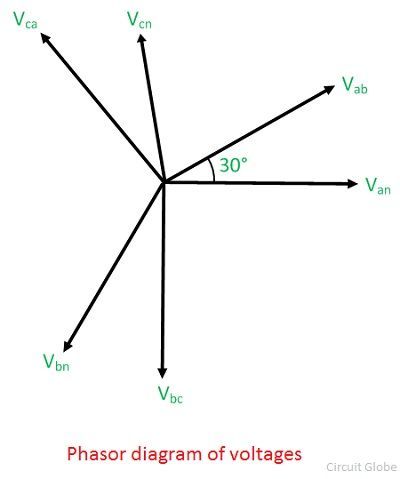
Ta spänningen från ledare a till neutral som referensfasor
Potentialdifferensen mellan ledare a och b kan skrivas som
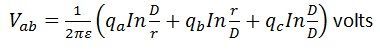
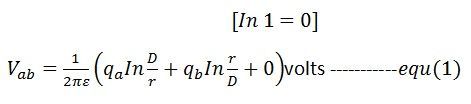Potentialdifferensen mellan ledare a och c är på samma sätt
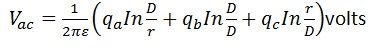
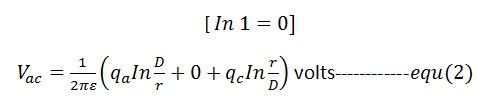Om man adderar ekvationerna (1) och (2), får vi
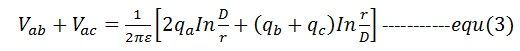Och,
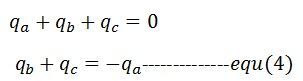Kombinera ekvation (3) och (4)
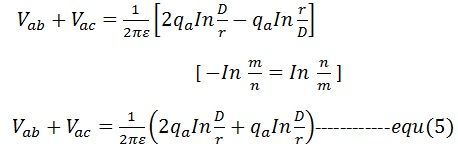
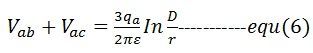
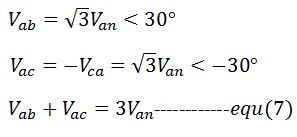Från ekvation (6) och (7)
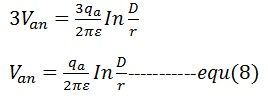Kapacitansen mellan linje och neutralledning
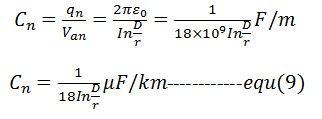Kapacitansen för en symmetrisk trefasledning är densamma som för en tvåtrådig ledning.