Alai

By Raymond Yuan, Software Engineering Intern

I den här handledningen kommer vi att lära oss hur man använder djupinlärning för att komponera bilder i stil med en annan bild (har du någonsin önskat att du kunde måla som Picasso eller Van Gogh?). Detta är känt som neuronal stilöverföring! Detta är en teknik som beskrivs i Leon A. Gatys artikel, A Neural Algorithm of Artistic Style, som är en bra läsning, och du bör definitivt kolla in den.

Neural style transfer är en optimeringsteknik som används för att ta tre bilder, en innehållsbild, en stilreferensbild (t.ex. ett konstverk av en berömd målare) och inmatningsbilden som du vill styla – och blanda dem så att inmatningsbilden omvandlas till att se ut som innehållsbilden, men ”målas” i stilen av stilbilden.

Till exempel tar vi en bild av denna sköldpadda och Katsushika Hokusais Den stora vågen utanför Kanagawa:

Nu hur skulle det se ut om Hokusai bestämde sig för att lägga till texturen eller stilen av sina vågor till bilden av sköldpaddan? Något liknande?

Är detta magi eller bara djupinlärning? Lyckligtvis handlar det inte om någon magi: stilöverföring är en rolig och intressant teknik som visar upp de neurala nätverkens kapacitet och interna representationer.

Principen för neuronal stilöverföring är att definiera två distansfunktioner, en som beskriver hur olika innehållet i två bilder är, Lcontent, och en som beskriver skillnaden mellan de två bilderna i termer av deras stil, Lstyle. Sedan, givet tre bilder, en önskad stilbild, en önskad innehållsbild och inmatningsbilden (initialiserad med innehållsbilden), försöker vi omvandla inmatningsbilden för att minimera innehållsavståndet med innehållsbilden och dess stilavstånd med stilbilden.

Sammanfattningsvis tar vi basinmatningsbilden, en innehållsbild som vi vill matcha, och stilbilden som vi vill matcha. Vi omvandlar den grundläggande inmatningsbilden genom att minimera innehålls- och stilavstånden (förlusterna) med backpropagation, vilket skapar en bild som matchar innehållet i innehållsbilden och stilen i stilbilden.

I processen kommer vi att bygga upp praktisk erfarenhet och utveckla intuition kring följande begrepp:

• Eager Execution – använd TensorFlows imperativa programmeringsmiljö som utvärderar operationer omedelbart
• Lär dig mer om eager execution
• Se det i praktiken (många av handledningarna kan köras i Colaboratory)
• Användning av Functional API för att definiera en modell – vi kommer att bygga en delmängd av vår modell som kommer att ge oss tillgång till nödvändiga mellanliggande aktiveringar med hjälp av Functional API
• Utnyttja funktionskartor för en förtränad modell – Lär dig att använda förtränade modeller och deras funktionskartor
• Skapa anpassade träningsloopar – vi undersöker hur man ställer in en optimerare för att minimera en given förlust med avseende på ingångsparametrar

Vi kommer att följa de allmänna stegen för att utföra stilöverföring:

1. Visualisera data
2. Grundläggande förbehandling/förberedelse av våra data
3. Sätt upp förlustfunktioner
4. Skapa modell
5. Optimera för förlustfunktion

Publik: Det här inlägget riktar sig till användare på mellannivå som är bekväma med grundläggande begrepp för maskininlärning. För att få ut det mesta av det här inlägget bör du:

• Läsa Gatys uppsats – vi förklarar på vägen, men uppsatsen ger en mer djupgående förståelse för uppgiften
• Förstå gradient descent

Tidsuppskattning: 60 min

Kod:

Den fullständiga koden för den här artikeln finns på den här länken. Om du vill gå igenom det här exemplet kan du hitta colab här.

Implementation

Vi börjar med att aktivera eager execution. Eager execution gör att vi kan arbeta igenom den här tekniken på det tydligaste och mest lättlästa sättet.

Definiera innehålls- och stilrepresentationer

För att få fram både innehålls- och stilrepresentationer av vår bild kommer vi att titta på några mellanliggande lager i vår modell. Mellanliggande lager representerar funktionskartor som blir allt högre ordnade när man går djupare. I det här fallet använder vi nätverksarkitekturen VGG19, ett förtränat bildklassificeringsnätverk. Dessa mellanliggande lager är nödvändiga för att definiera representationen av innehåll och stil från våra bilder. För en inmatningsbild kommer vi att försöka matcha motsvarande målrepresentationer för stil och innehåll i dessa mellanliggande lager.

Varför mellanliggande lager?

Du kanske undrar varför dessa mellanliggande utgångar i vårt förtränade bildklassificeringsnätverk gör det möjligt för oss att definiera stil- och innehållsrepresentationer. På en hög nivå kan detta fenomen förklaras med att för att ett nätverk ska kunna utföra bildklassificering (vilket vårt nätverk har tränats att göra) måste det förstå bilden. Detta innebär att ta den råa bilden som ingångspixlar och bygga upp en intern representation genom transformationer som förvandlar de råa bildpixlarna till en komplex förståelse av de egenskaper som finns i bilden. Detta är också delvis anledningen till att konvolutionella neurala nätverk kan generalisera väl: de kan fånga invarianter och definierande egenskaper inom klasser (t.ex. katter vs. hundar) som är oberoende av bakgrundsbrus och andra olägenheter. Någonstans mellan det ställe där råbilden matas in och klassificeringsetiketten matas ut fungerar modellen alltså som en komplex funktionsextraktor; genom att få tillgång till mellanliggande lager kan vi alltså beskriva innehållet och stilen i ingångsbilderna.

Specifikt kommer vi att dra ut dessa mellanliggande lager från vårt nätverk:

Modell

I det här fallet laddar vi VGG19, och matar in vår inmatningstensor till modellen. På så sätt kan vi extrahera funktionskartor (och därefter innehålls- och stilrepresentationer) för innehåll, stil och genererade bilder.

Vi använder VGG19, som föreslås i artikeln. Dessutom, eftersom VGG19 är en relativt enkel modell (jämfört med ResNet, Inception etc.) fungerar funktionskartorna faktiskt bättre för stilöverföring.

För att få tillgång till de mellanliggande lagren som motsvarar våra stil- och innehållsfunktionskartor får vi motsvarande utgångar genom att använda Keras Functional API för att definiera vår modell med önskade utgångsaktiveringar.

Med Functional API innebär definiering av en modell helt enkelt att man definierar input och output: model = Model(inputs, outputs).

I ovanstående kodutdrag laddar vi vårt förtränade bildklassificeringsnätverk. Sedan tar vi tag i de lager av intresse som vi definierade tidigare. Sedan definierar vi en modell genom att ställa in modellens ingångar till en bild och utgångarna till utgångarna från stil- och innehållslagren. Med andra ord har vi skapat en modell som kommer att ta en ingångsbild och ge ut innehålls- och stilmellanlagren!

Definiera och skapa våra förlustfunktioner (innehålls- och stilavstånd)

Vår definition av innehållsförlust är faktiskt ganska enkel. Vi ger nätverket både den önskade innehållsbilden och vår basingångsbild. Detta kommer att returnera mellanlagrens utdata (från de lager som definierats ovan) från vår modell. Sedan tar vi helt enkelt det euklidiska avståndet mellan de två mellanliggande representationerna av dessa bilder.

Mer formellt sett är innehållsförlust en funktion som beskriver avståndet mellan innehållet från vår ingångsbild x och vår innehållsbild, p . Låt Cₙₙ vara ett förtränat djupt konvolutionellt neuralt nätverk. I det här fallet använder vi återigen VGG19. Låt X vara en bild, så är Cₙₙ(x) det nätverk som matas av X. Låt Fˡᵢⱼ(x)∈ Cₙₙ(x)och Pˡᵢⱼ(x) ∈ Cₙₙ(x) beskriva respektive mellanliggande funktionsrepresentation av nätverket med ingångarna x och p på lager l . Sedan beskriver vi innehållsavståndet (förlusten) formellt som:

Vi utför backpropagation på sedvanligt sätt så att vi minimerar denna innehållsförlust. Vi ändrar alltså den ursprungliga bilden tills den genererar ett liknande svar i ett visst lager (definierat i content_layer) som den ursprungliga innehållsbilden.

Detta kan genomföras ganska enkelt. Återigen tar den som indata funktionskartorna i ett lager L i ett nätverk som matas av x, vår ingångsbild, och p, vår innehållsbild, och returnerar innehållsavståndet.

Stilförlust:

Beräkningen av stilförlust är lite mer komplicerad, men följer samma princip, den här gången matas vårt nätverk med den grundläggande ingångsbilden och stilbilden. Men i stället för att jämföra de råa mellanliggande utgångarna av basingångsbilden och stilbilden jämför vi istället Gram-matriserna för de två utgångarna.

Matematiskt beskriver vi stilförlusten för basingångsbilden x och stilbilden a som avståndet mellan stilrepresentationerna (Gram-matriserna) för dessa bilder. Vi beskriver stilrepresentationen av en bild som korrelationen mellan olika filtersvar som ges av Grammatrisen Gˡ, där Gˡᵢⱼ är den inre produkten mellan den vektoriserade funktionskartan i och j i lager l. Vi kan se att Gˡᵢⱼ som genereras över funktionskartan för en given bild representerar korrelationen mellan funktionskartorna i och j.

För att generera en stil för vår basingångsbild utför vi gradientnedgång från innehållsbilden för att omvandla den till en bild som matchar stilrepresentationen av den ursprungliga bilden. Det gör vi genom att minimera det genomsnittliga kvadratiska avståndet mellan funktionen korrelationskartan för stilbilden och ingångsbilden. Varje skikts bidrag till den totala stilförlusten beskrivs av

där Gˡᵢⱼ och Aˡᵢⱼ är den respektive stilrepresentationen i skikt l av ingångsbild x och stilbild a. Nl beskriver antalet funktionskartor, var och en av storleken Ml=höjd∗bredd. Den totala stilförlusten i varje lager är således

där vi viktar bidraget från varje lagers förlust med någon faktor wl. I vårt fall viktar vi varje lager lika:

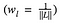
Detta genomförs enkelt:

Run Gradient Descent

Om du inte är bekant med gradient descent/backpropagation eller behöver en uppfräschning bör du definitivt kolla in denna resurs.

I det här fallet använder vi Adam-optimeringen för att minimera förlusten. Vi uppdaterar iterativt vår utgångsbild så att den minimerar vår förlust: vi uppdaterar inte vikterna som är kopplade till vårt nätverk, utan tränar istället vår ingångsbild för att minimera förlusten. För att kunna göra detta måste vi veta hur vi beräknar vår förlust och våra gradienter. Observera att L-BFGS-optimeringen, som om du är bekant med den här algoritmen rekommenderas, men som inte används i den här handledningen eftersom en primär motivation bakom den här handledningen var att illustrera bästa praxis med eager exekvering. Genom att använda Adam kan vi demonstrera autograd/gradientband-funktionaliteten med anpassade träningsslingor.

Beräkna förlusten och gradienterna

Vi kommer att definiera en liten hjälpfunktion som kommer att läsa in vår innehålls- och stilbild, mata dem framåt genom vårt nätverk, som sedan kommer att ge ut innehålls- och stilfunktionsrepresentationerna från vår modell.

Här använder vi tf.GradientTape för att beräkna gradienten. Det gör att vi kan dra nytta av den automatiska differentiering som finns tillgänglig genom spårningsoperationer för att beräkna gradienten senare. Den registrerar operationerna under den framåtriktade passagen och kan sedan beräkna gradienten för vår förlustfunktion med avseende på vår inmatningsbild för den bakåtriktade passagen.

Då är det enkelt att beräkna gradienterna:

Applicera och kör stilöverföringsprocessen

Och för att faktiskt utföra stilöverföringen:

Och så är det!

Låt oss köra den på vår bild av sköldpaddan och Hokusais Den stora vågen utanför Kanagawa:

Se den iterativa processen över tid:

Här är några andra häftiga exempel på vad neuronal stilöverföring kan göra. Kolla in det!

Try out your own images!

Vad vi täckte:

• Vi byggde flera olika förlustfunktioner och använde backpropagation för att omvandla vår inmatningsbild för att minimera dessa förluster.
• För att göra detta laddade vi in en förtränad modell och använde dess inlärda funktionskartor för att beskriva innehållet och stilrepresentationen av våra bilder.
• Våra viktigaste förlustfunktioner var främst att beräkna avståndet i termer av dessa olika representationer.
• Vi implementerade detta med en anpassad modell och eager execution.
• Vi byggde vår anpassade modell med Functional API.
• Eager execution gör det möjligt för oss att arbeta dynamiskt med tensorer, med hjälp av ett naturligt python-kontrollflöde.
• Vi manipulerade tensorer direkt, vilket underlättar felsökning och arbete med tensorer.

Vi uppdaterade bilden iterativt genom att tillämpa våra uppdateringsregler för optimerare med hjälp av tf.gradient. Optimeraren minimerade de givna förlusterna med avseende på vår inmatningsbild.