Alai

Michael Fowler,UVa Physics.

Momentum har riktning

Som vi diskuterade i förra föreläsningen hade Descartes, redan innan Newton formulerade sina lagar, med lite hjälp av Huygens, upptäckt en djupdynamisk sanning: i varje kollision, eller i själva verket i varje växelverkan av något slag, förblev den totala mängden ”momentum” – ett mått på rörelse – alltid densamma. Impulsen hos ett rörligt föremål definieras som produkten av massan och hastigheten och är således en vektor: den har storlek och riktning. Om du står på friktionsfria skridskor och kastar en boll rör du dig bakåt: du har ett moment som är lika stort som bollens, men har motsatt riktning, så det totala momentet (ditt plus bollens) förblir noll. Raketer fungerar på samma sätt genom att de kastar ut material med hög hastighet. De fungerar inte genom att ”trycka mot luften”, utan genom att trycka mot det material de skjuter ut, på samma sätt som du trycker mot en boll du kastar och den trycker dig tillbaka och orsakar din acceleration.

Om du fortfarande misstänker att raketer verkligen trycker mot luften, kom ihåg att de fungerar lika bra i rymden! Faktum är att många trodde att när Goddard, en tidig amerikansk raketforskare (Goddard Space Flight Center är uppkallat efter honom) pratade om raketer i rymden, så slösade han bort sin tid. Jag citerar från en ledare i New York Times från 1921: ”Professor Goddard känner inte till förhållandet mellan handling och reaktion och behovet av att ha något bättre än ett vakuum att reagera mot. Han verkar sakna den grundläggande kunskap som dagligen delas ut i våra gymnasieskolor.” Det är uppenbart att New York Times ledarskribenter vid den tiden inte gillade den grundläggande kunskap som delades ut i denna kurs!

Som vi diskuterade följer faktiskt bevarandet av rörelsemängden vid en kollision av Newtons lagar. Det är dock ett mer allmänt och enklare begrepp – det är inte alls beroende av detaljerna i växelverkan osv. Denna enkelhet tilltalade uppenbarligen Einstein, som var övertygad om att när dynamiken omformulerades för att inkludera de nya idéerna om tid och rum, borde bevarandet av rörelsemängden fortfarande gälla i alla tröghetsramar. Detta ledde honom till några överraskande slutsatser, som vi kommer att se.

Momentumbevarande på biljardbordet

Som en uppvärmningsövning ska vi betrakta momentumbevarande för en kollision mellan två bollar på ett biljardbord. Vi ritar en kritlinje i mitten av biljardbordet och skjuter bollarna nära, men på motsatta sidor av kritlinjen från vardera änden, med samma hastighet, så att de kommer att träffa varandra i mitten med ett slående slag, vilket kommer att vrida deras hastigheter i en liten vinkel. Med andra ord, om vi från början säger att deras hastigheter (lika stora, motsatt riktning) var parallella med x-riktningen – kritstrecket – så kommer de efter kollisionen också att ha lika stora och motsatta små hastigheter i y-riktningen (hastigheterna i x-riktningen kommer att ha minskat mycket lite).

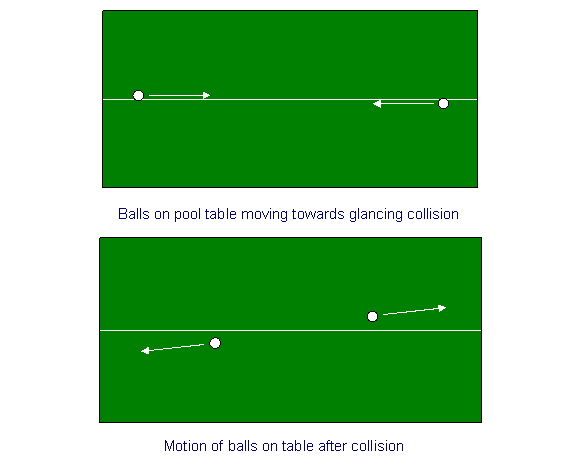
En symmetrisk rymdskeppskollision

Nu ska vi upprepa övningen i stor skala. Anta att vi någonstans i rymden, långt från alla gravitationsfält, sätter ut ett snöre som är en miljon mil långt. (Det skulle kunna vara mellan våra två klockor i tidsutvidgningsexperimentet). Detta snöre motsvarar kritstrecket på biljardbordet. Anta att vi nu har två identiska rymdskepp som närmar sig varandra med samma och motsatta hastigheter parallellt med snöret från snörets båda ändar, och som är riktade så att de drabbas av en liten glidande kollision när de möts i mitten. Det framgår av situationens symmetri att rörelsemängden bevaras i båda riktningarna. I synnerhet är den hastighet med vilken det ena rymdskeppet rör sig bort från snöret efter kollisionen – dess y-hastighet – lika stor som den hastighet med vilken det andra rymdskeppet rör sig bort från snöret.

Men betrakta nu denna kollision som den observeras av någon i ett av rymdskeppen, kalla det A. Före kollisionen ser han strängen röra sig mycket snabbt vid fönstret, säg några meter bort. Efter kollisionen ser han att snöret rör sig iväg med, låt oss säga, 15 meter per sekund. Detta beror på att rymdskepp A har fått en hastighet vinkelrätt mot snöret på 15 meter per sekund. Eftersom detta är en fullständigt symmetrisk situation skulle en observatör på rymdskepp B med säkerhet dra slutsatsen att hennes rymdskepp också rörde sig bort från snöret med en hastighet av 15 meter per sekund.

Hur symmetriskt är det?

Den avgörande frågan är: hur snabbt ser en observatör på rymdskepp A att rymdskepp B rör sig bort från snöret? Låt oss anta att i förhållande till rymdskepp A rör sig rymdskepp B bort (i x-riktningen) med 0,6c. Först ska vi komma ihåg att avstånd vinkelrätt mot rörelseriktningen inte är Lorentz-kontraherade. När observatören i rymdskepp B säger att hon har rört sig 15 meter längre bort från snöret under ett intervall på en sekund, kommer observatören som iakttar denna rörelse från rymdskepp A att hålla med om de 15 metrarna – men inte hålla med om den ena sekunden! Han kommer att säga att hennes klockor går långsamt, så enligt hans klockor har det gått 1,25 sekunder när hon rör sig 15 meter i y-riktningen.

Det följer att, som ett resultat av tidsutvidgningen, orsakar denna kollision sett från rymdskepp A inte lika och motsatta hastigheter för de två rymdskeppen i y-riktningen. Ursprungligen rörde sig båda rymdskeppenparallellt med x-axeln, det fanns nollmomentum i y-riktningen. Hur kan vi då hävda att det finns ett totalt momentum på noll i y-riktningen efter kollisionen, när de identiska rymdskeppen inte har lika och motsatta hastigheter?

Einstein räddar momentumbevarande

Einstein var så säker på att momentumbevarande alltid måste gälla att han räddade det med en djärv hypotes: massan hos ett föremål måste bero på dess hastighet! I själva verket måste massan öka med hastigheten på ett sådant sätt att den lägre hastigheten i y-riktningen till följd av tidsutvidgningen upphävs. Det vill säga, om ett objekt i vila har en massa m och rör sig med en hastighet v kommer det att ha en tröghet som motsvarar en ”relativistisk massa” m rel =m/ 1-( v 2 / c 2 ) .Då blir rörelsemängden

p → = m rel v → =m v → / 1-( v 2 / c 2 ) .

Notera att denna relativistiska massökning är en obetydligt liten effekt vid vanliga hastigheter, men när ett föremål närmar sig flyghastigheten ökar massan obegränsat!

Massan ökar verkligen med hastigheten

Att bestämma att objektens massa måste bero på hastigheten på detta sätt verkar vara ett högt pris att betala för att rädda rörelsemängdens bevarande! Det är emellertid en förutsägelse som inte är svår att kontrollera genom experiment. Den första bekräftelsen kom 1908 genom att avleda snabba elektroner i ett vakuumrör. I själva verket har elektronerna i ett gammalt färgtv-rör ungefär en halv procent mer tröghet än elektroner i vila, och detta måste tas med i beräkningen av de magnetfält som används för att styra dem till skärmen.

I moderna partikelacceleratorer används mycket kraftiga elektriska fält för att accelerera elektroner, protoner och andra partiklar. I praktiken visar det sig att dessa partiklar behöver allt större krafter för att accelereras ytterligare när ljusets hastighet närmar sig. Ljusets hastighet är därför en naturlig absolut hastighetsgräns. Partiklar accelereras till hastigheter där deras relativistiska massa är tusentals gånger större än deras massa i vila, vanligtvis kallad ”vilomassa”.

…eller gör den det?

Det pågår faktiskt en ständig debatt bland fysikerna om begreppet relativistisk massa. Debatten är till stor del semantisk: ingen tvivlar på att det korrekta uttrycket för rörelsemängden hos en partikel med vilomassa m som rör sig med hastigheten v → är p → = m 1- v 2 / c 2 v → . Men framför allt partikelfysiker, av vilka många tillbringar sina liv med att mäta partiklars vilomassa med stor precision, är inte förtjusta i att skriva detta som p → = m rel v → . De gillar inte tanken på en variabel massa. För det första kan det ge intryck av att en partikel blir större när den ökar i hastighet, eller att åtminstone dess inre struktur förändras på något sätt. I själva verket genomgår en relativistisk partikel bara en Lorentz-kontraktion längs rörelseriktningen, precis som allt annat. Den går från en sfärisk form till en skivform med samma tvärgående radie.

Så hur kan denna ”massökning” förstås? Som vanligt hade Einstein rätt: han påpekade att varje form av energi har tröghet. Själva den kinetiska energin har tröghet. Nu är ”tröghet” en definierande egenskap hos massan. Den andra grundläggande egenskapen hos massan är att den drar till sig gravitationen. Gör denna kinetiska energi det? För att se svaret kan man betrakta en sfär fylld med gas. Den kommer att generera ett sfäriskt symmetriskt gravitationsfält utanför sig själv, vars styrka är proportionell mot den totala massan. Om vi nu värmer upp gasen kommer gaspartiklarna att ha denna ökade (relativistiska) massa, som motsvarar deras ökade rörelseenergi, och det yttre gravitationsfältet kommer att ha ökat proportionellt. (Ingen betvivlar detta.)

Så den ”relativistiska massan” har verkligen de två grundläggande massegenskaperna: tröghet och gravitationsdragningskraft. (Som kommer att framgå i de följande föreläsningarna är denna relativistiska massa inget annat än den totala energin, där själva vilomassan nu ses som energi.)

På en mer trivial nivå motsätter sig en del lärare att införa den relativistiska massan eftersom de är rädda att eleverna kommer att anta att den kinetiska energin hos en relativistiskt rörlig partikel bara är 1 2 m v → 2 med hjälp av den relativistiska massan – men så är det inte, vilket vi kommer att se inom kort.

Fotnot: För alla som kanske någon gång går vidare till en morematematiskt sofistikerad behandling bör det tilläggas att vilomassan spelar en viktig roll som en invariant när man går från en referensram till en annan, men den ”relativistiska massan” som används här är egentligen bara den första komponenten (energin) av den fyrdimensionella energimomentvektorn för en partikel, och är alltså inte en invariant.

Kinetisk energi och massa för mycket snabba partiklar

Vi tänker på den kinetiska energin hos en av dessapartiklar som färdas nära ljusets hastighet. Kom ihåg att vi i en tidigare föreläsning fann att den kinetiska energin för en vanlig icke-relativistisk (dvs. långsamt rörlig) massa m var 1 2 m v 2 . Det sättet vi gjorde det på var genom att fundera över hur mycket arbete vi måste utföra för att lyfta den till en viss höjd: vi måste utöva en kraft som är lika stor som dess vikt W för att lyfta den till höjden h. Det totala arbetet, eller den energi som läggs ned, är kraft x avstånd, Wh. När den föll ner igen utförde gravitationskraften W exakt lika mycket arbete Wh på det fallande föremålet, men den här gången gick arbetet åt till att accelerera föremålet och ge det kinetisk energi. Eftersom vi vet hur snabbt fallande föremål tar sig upp, kunde vi dra slutsatsen att den kinetiska energin var 1 2 m v 2 . (För detaljer, se föregående föreläsning.)

Mer generellt sett kunde vi ha accelererat massan med vilkenkonstant kraft F som helst, och funnit det arbete som kraften utförde (kraft x avstånd) för att få den att nå hastigheten v från en stående start. Massans kinetiska energi, E= 1 2 m v 2 , är exakt lika med det arbete som utförs av kraften för att få upp massan till den hastigheten. (Det kan visas på liknande sätt att om en kraft appliceras på en partikel som redan rör sig med hastigheten u, låt oss säga, och den accelereras till hastigheten v, är det nödvändiga arbetet 1 2 m v 2 – 1 2 m u 2 .)

Det är intressant att försöka upprepa övningen för en partikel som rör sig mycket nära ljusets hastighet, som partiklarna i de acceleratorer som nämns i föregående stycke. Newtons andra lag, i formen

Kraft = rörelsemängdens förändringshastighet

är fortfarande sann, men nära ljusets hastighet förändras hastigheten försumbart när kraften fortsätter att verka – i stället ökar massan! Därför kan vi skriva till en utmärkt approximation:

Kraft = (massans förändringshastighet) x c

där c som vanligt är ljusets hastighet. För att bli mer specifik antar vi att vi har en konstant kraft F som trycker på en partikel. I ett visst ögonblick har partikeln massa M och en hastighet som ligger extremt nära c. En sekund senare, eftersom kraften fortsätter att arbeta på partikeln, och därmed ökar dess rörelsemängd enligt Newtons andra lag, kommer partikeln att ha massa M+m, där m är ökningen av massan till följd av det arbete som utförs av kraften.

Vad är ökningen av partikelns rörelseenergi E under denna ensekundersperiod? I exakt analogi med det icke-relativistiska fallet som vi granskat ovan är det bara det arbete som utförs av kraften under denna period. Eftersom partikelns massa förändras med m under en sekund är m också massans förändringshastighet. Därför kan vi utifrån Newtons andra lag i formen

Kraft = (massans förändringshastighet) x c,

skriva

Kraft =mc.

Ökningen av den kinetiska energin E under en sekund är bara det arbete som utförs av kraften,

E= kraft x avstånd.

Då partikeln rör sig i stort sett med flyghastighet är det avstånd som kraften verkar över under en sekund bara c meter, c=3× 10 8 .

Det totala arbete som kraften utför under den sekunden är alltså kraft x avstånd =mc×c=m c 2 .

Därmed är förhållandet mellan ökningen av massan hos den relativistiska partikeln och ökningen av dess rörelseenergi följande:

E=m c 2 .

Kinetisk energi och massa för långsamma partiklar

Håll dig i minnet att för att få Newtons lagar att gälla i alla tröghetsramar var vi tvungna att anta en ökning av massan med hastigheten med faktorn 1/ 1-( v 2 / c 2 ) . Detta innebär att även ett föremål som rör sig långsamt har en liten ökning av massan när det rör sig!

Hur förhåller sig denna lilla ökning till den kinetiska energin? Betrakta en massa M som rör sig med hastigheten v, som är mycket mindre än ljusets hastighet. Dess kinetiska energi E= 1 2 M v 2 , som diskuterats ovan. Dess massa är M/ 1-( v 2 / c 2 ) , vilket vi kan skriva som M+m. Vad är m?

Då vi talar om hastigheter som vi är bekanta med, som ett jetplan, där v/c, är mycket litet, kan vi använda några enkla matematiska knep för att göra det lättare.

Den första är en bra approximation för kvadratroten av 1-x när x är mycket mindre än ett:

1-x ≅1- 1 2 x för x≪1.

Du kan enkelt kontrollera detta med din miniräknare: prova x= 1 100 , du finner 99 100 =0,994987… vilket är extremt nära 1- 1 2 1 100 =0,995 !

Nästa approximation är

1 1-x ≅1+x för x≪1.

Detta är också lätt att kontrollera: ta återigen x= 1 100 : 1 1 1-x = 1 99 100 = 100 99 = 100 99 =1,01010… ,och 1+x= 101 100 =1,01.

Med hjälp av dessa approximationer med x=v/c kan vi approximera 1-( v 2 / c 2 ) som 1- 1 2 ( v 2 / c 2 ) ,och sedan 1/( 1- 1 2 ( v 2 / c 2 ) ) som 1+ 1 2 ( v 2 / c 2 ) .

Detta innebär att den totala massan vid hastigheten v

M 1-( v 2 / c 2 ) ≅M( 1+ 1 2 ( v 2 / c 2 ) ),

och genom att skriva detta som M+m, ser vi att massökningen m är lika med 1 2 M v 2 / c 2 .

Detta innebär att – återigen – massökningen m är relaterad till den kinetiska energin E genom E=m c 2 .

Det är faktiskt inte svårt att visa, med hjälp av lite kalkyl, att över hela hastighetsområdet från noll till så nära ljusets hastighet som möjligt, upplever en partikel i rörelse en massökning som är relaterad till dess kinetiska energi med E=m c 2 . För att förstå varför detta inte märks i vardagen kan du prova ett exempel, t.ex. ett jetflygplan som väger 100 ton och rör sig i en hastighet av 2 000 mph. 100 ton är 100 000 kilo, 2 000 mph är ungefär 1 000 meter per sekund. Det är en kinetisk energi 1 2 M v 2 på ½ ×1011 joule, men den motsvarande massförändringen hos flygplanet är lägre med faktorn c 2 , 9 × 10 16 , vilket ger en faktisk massökning på ungefär ett halvt milligram, vilket inte är så lätt att upptäcka!

E = mc2

Vi har sett ovan att när en kraft utför ett arbete som accelererar en kropp för att ge den rörelseenergi, ökar kroppens massa med ett belopp som är lika med det totala arbete som utförs av kraften, den överförda energin E, dividerat med c 2 . Hur är det då när en kraft utför ett arbete på en kropp som inte ökar dess hastighet, så att den kinetiska energin inte ökar? Vad händer till exempel om jag bara lyfter något i jämn takt, vilket ger det potentiell energi? Det visar sig att det även i detta fall sker en ökning av massan enligt E=m c 2 , som naturligtvis är mycket liten för vardagliga föremål.

Detta är dock en mätbar och viktig effekt inom kärnfysiken. Heliumatomen har till exempel en kärna med två protoner och två neutroner som är mycket hårt bundna till varandra genom en stark kärnkraft. Om tillräcklig yttre kraft tillämpas kan den delas upp i två ”tunga vätekärnor”, som var och en har en proton och en neutron. Mycket yttre energi måste användas för att uppnå denna separation, och man finner att den totala massan av de två tunga vätekärnorna är mätbart (ungefär en halv procent) tyngre än den ursprungliga heliumkärnan. Denna extramassa, multiplicerad med c 2 , är precis lika stor som den energi som behövs för att dela heliumkärnan i två delar. Ännu viktigare är att denna energi kan återvinnas genom att låta de två tunga vätekärnorna kollidera och förenas för att bilda en heliumkärna igen. (De är båda elektriskt positivt laddade, så de stöter bort varandra, och måste komma samman ganska snabbt för att övervinna denna avstötning och komma till den närhet där den mycket starkare kärnkraftsattraktionen kommer in.) Detta är den grundläggande kraftkällan i vätebomben och i solen.

Det visar sig att alla former av energi, kinetisk och olika typer av potentiell energi, har en tillhörande massa som ges av E=m c 2 . För kärnreaktioner är massförändringen typiskt sett i storleksordningen en tusendedel av den totala massan, och den är lätt att mäta. För kemiska reaktioner är förändringen av storleksordningen en miljarddel av den totala massan och kan för närvarande inte mätas.

förra index